Figuras geométricas: imágenes y dibujos para aprender y jugar

Última actualización junio 29, 2020

Probablemente hayas aprendido mucho sobre las figuras geométricas sin pensar realmente en qué son. En este artículo, les enseñaremos cuáles son las más comunes, sus aspectos y las fórmulas principales asociadas a ellas. Además, les dejaremos una gran cantidad de imágenes y dibujos para que puedan aprender de una forma didáctica y super divertida.

¿Qué es una figura geométrica?

En geometría, una figura geométrica se puede definir como la forma de un objeto, su contorno, límite exterior o superficie exterior. Todo lo que vemos en el mundo que nos rodea tiene una forma. Podemos encontrar algunas formas básicas como el cuadrado, el rectángulo y el óvalo o el prisma rectangular, el cilindro y la esfera en los objetos que vemos a nuestro alrededor. Ejemplos que vemos cotidianamente son tarjetas de crédito, billetes y monedas, anillos para los dedos, marcos de fotos, tableros de dardos, ventanas, edificios, macetas, trenes de juguete, globos y millones de cosas más.

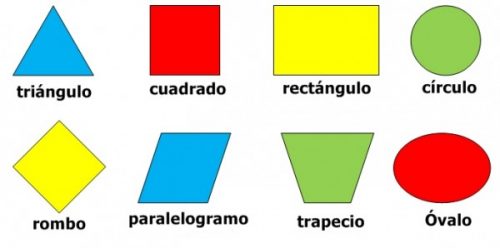
Figuras geométricas y sus nombres

Tipo 1: Elipses

Las elipses son formas redondas y ovaladas en las que un punto dado (p) tiene la misma suma de distancia desde dos focos diferentes.

Óvalo

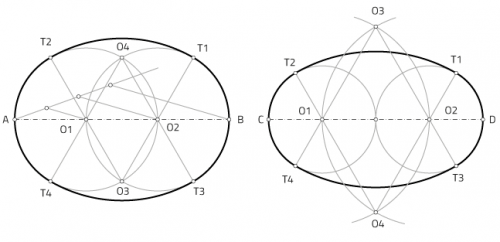
Un óvalo se parece un poco a un círculo pero, en lugar de ser perfectamente redondo, se ensancha de alguna manera. Sin embargo, la clasificación es imprecisa. Hay muchos, muchos tipos de óvalos, pero el significado general es que son una forma redonda alargada en lugar de perfectamente redonda, como lo es un círculo.

Debido a que un óvalo no es perfectamente redondo, las fórmulas que usamos para comprenderlos tienen que ajustarse.

También es importante tener en cuenta que calcular la circunferencia de un óvalo es bastante difícil, por lo que no dejaremos una ecuación para ello a continuación. En su lugar, use una calculadora en línea con una función de circunferencia incorporada, porque incluso las mejores ecuaciones existentes solo darán como resultado aproximaciones.

Definiciones

• Radio mayor: la distancia desde el origen del óvalo hasta el borde más alejado
• Radio menor: la distancia desde el origen del óvalo hasta el borde más cercano

Fórmulas

• Área = Radio mayor * Radio menor * π

Circulo

¿Cuántos lados tiene un círculo? ¡Buena pregunta! Desafortunadamente, no hay una respuesta, porque los «lados» tienen más que ver con los polígonos: una forma bidimensional con al menos tres lados rectos y típicamente al menos cinco ángulos. Los círculos no tienen lados rectos y definitivamente carecen de cinco ángulos, por lo que no son polígonos.

Entonces, ¿cuántos lados tiene un círculo? ¿Cero? ¿Uno? Es irrelevante, en realidad, la pregunta simplemente no se aplica a los círculos.

Un círculo no es un polígono, pero ¿qué es? Un círculo es una forma bidimensional (no tiene grosor ni profundidad) formada por una curva que siempre está a la misma distancia de un punto en el centro. Un óvalo tendrá medida diferentes si te posicionas en dos puntos, mientras que los focos de un círculo siempre están en la misma posición.

Definiciones

• Origen: el punto central del círculo.
• Radio: la distancia desde el origen a cualquier punto del círculo.
• Circunferencia: la distancia alrededor del círculo
• Diámetro: la longitud de un borde del círculo al otro

Fórmulas

• Circunferencia = π * radio
• Área = π * radio ^ 2

Tipo 2: Triángulos

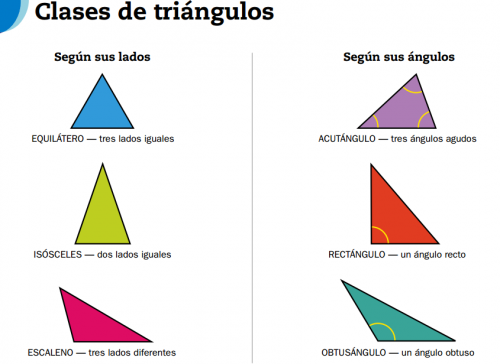
Los triángulos son los polígonos más simples. Tienen tres lados y tres ángulos, pero pueden verse diferentes el uno del otro. Es posible que haya oído hablar de triángulos rectángulos o triángulos isósceles: son diferentes tipos de triángulos, pero todos tendrán tres lados y tres ángulos.

Debido a que hay muchos tipos de triángulos, hay muchas fórmulas importantes, algunas más complejas que otras. Los elementos básicos se mostrarán a continuación y se basan en conocer la longitud de los lados. Si no conoce esto ultimo, aún puede calcular diferentes aspectos del mismo utilizando ángulos o solo algunos de los lados.

Definiciones

• Vértice: el punto donde se encuentran dos lados de un triángulo
• Base: cualquiera de los lados del triángulo, típicamente el dibujado en la parte inferior
• Altura: la distancia vertical desde una base a un vértice al que no está conectado

Fórmulas

• Área = (base * altura) / 2
• Perímetro = lado a + lado b + lado c

Tipo 3: Paralelogramos

Un paralelogramo es una forma con ángulos opuestos iguales, lados opuestos paralelos y lados paralelos de igual longitud. Puede notar que esta definición se aplica a cuadrados y rectángulos, ¡porque estos ultimos también son paralelogramos! Si puede calcular el área de un cuadrado, puede hacerlo con cualquier paralelogramo.

Definiciones

• Longitud: la medida del lado inferior o superior de un paralelogramo
• Ancho: la medida del lado izquierdo o derecho de un paralelogramo

Fórmulas

• Área: longitud * altura
• Perímetro: Lado1 + Lado2 + Lado3 + Lado4
• Alternativamente, Perímetro: Lado * 4

Rectángulo

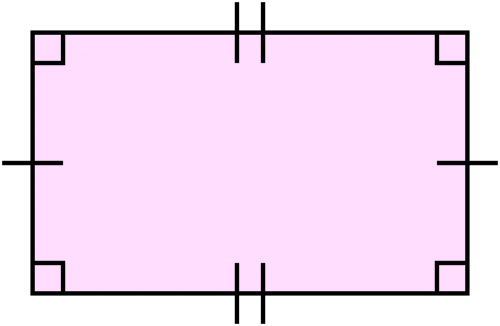
Un rectángulo es una forma con lados opuestos paralelos, combinados con todos los ángulos de 90 grados. Como es un tipo de paralelogramo, tiene lados paralelos opuestos (unos más largos que otros, por lo que parece un cuadrado alargado).

Debido a que un rectángulo es un paralelogramo, puede usar exactamente las mismas fórmulas para calcular su área y perímetros.

Cuadrado

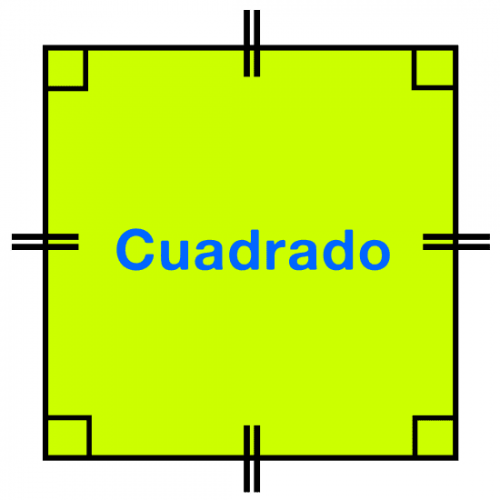
Un cuadrado es muy parecido a un rectángulo, con una notable excepción: todos sus lados tienen la misma longitud. Al igual que los rectángulos, los cuadrados tienen ángulos de 90 grados y lados opuestos paralelos. ¡Eso es porque un cuadrado es en realidad un tipo de rectángulo, que a su vez es un tipo de paralelogramo!

Por esa razón, puede usar las mismas fórmulas para calcular el área o el perímetro de un cuadrado como lo haría para cualquier otro paralelogramo.

Rombo

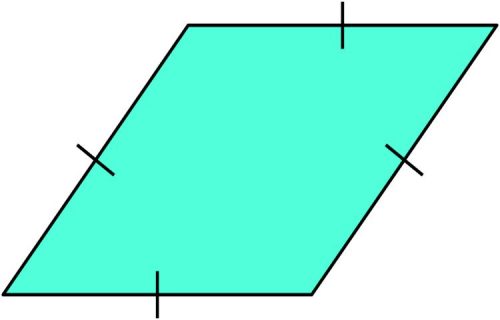
Un rombo es, lo has adivinado, un tipo de paralelogramo. La diferencia entre un rombo y un rectángulo o cuadrado es que sus ángulos interiores son solo los mismos que sus opuestos diagonales.

Debido a esto, un rombo se parece un poco a un cuadrado o rectángulo sesgado un poco hacia un lado. Aunque el perímetro se calcula de la misma manera, esto afecta la forma en que calcula el área, porque la altura ya no es la misma que sería en un cuadrado o rectángulo.

Definiciones

• Diagonal: la longitud entre dos vértices opuestos

Fórmulas

• Área = (Diagonal1 * Diagonal2) / 2

Tipo 4: Trapecios

Los trapecios son figuras de cuatro lados con dos lados paralelos opuestos. A diferencia de un paralelogramo, un trapecio tiene solo dos lados paralelos opuestos en lugar de cuatro, lo que afecta la forma en que calcula el área y el perímetro.

Definiciones

• Base: cualquiera de los lados paralelos de un trapecio
• Lado: cualquiera de los trapecios no laterales paralelos
• Altitud: la distancia de una base a la otra.

Fórmulas

• Área: [(Base1 * longitud + Base2 * longitud) / 2] * altitud
• Perímetro: Base + Base + Lado + Lado

Tipo 5: Pentágonos

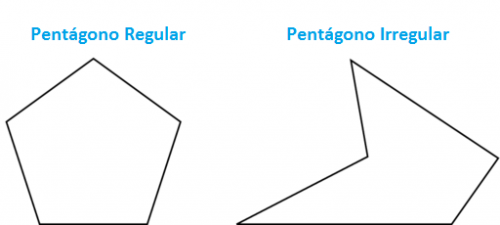
Un pentágono es una forma de cinco lados. Normalmente vemos pentágonos regulares, donde todos los lados y ángulos son iguales, pero también existen pentágonos irregulares. Estos últimos tienen lados desiguales y ángulos desiguales, y pueden ser convexos, sin ángulos apuntando hacia adentro, o cóncavos, con un ángulo interno mayor de 180 grados.

Debido a que la forma es más compleja, debe dividirse en formas más pequeñas para calcular su área.

Definiciones

• Apotema: una línea dibujada desde el centro del pentágono a uno de los lados, golpeando el lado en un ángulo recto.

Fórmulas

• Perímetro: Lado1 + Lado2 + Lado3 + Lado4 + Lado5
• Área: (perímetro * apotema) / 2

Tipo 6: hexágonos

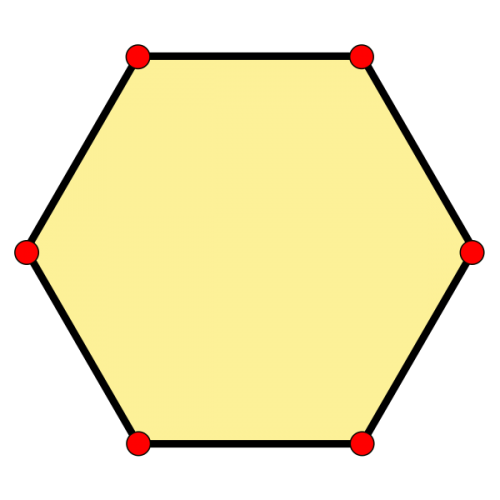
Un hexágono es una forma de seis lados que es muy similar al pentágono. La mayoría de las veces vemos hexágonos regulares, pero ellos, como los pentágonos, también pueden ser irregulares y convexos o cóncavos.

También como los pentágonos, la fórmula del área de un hexágono es significativamente más compleja que la de un paralelogramo.

Fórmulas

• Perímetro: Lado1 + Lado2 + Lado3 + Lado4 + Lado5 + Lado6
• Área: (perímetro * apotema) / 2

Figuras geométricas dibujos

Dibujos hechos con formas geométricas para colorear

Dibujos para colorear hechos con figuras geométricas

Dibujos de formas geométricas para descargar y colorear

Dibujo de elefante hecho con formas geométricas para pintar

Imagen de dibujos hechos con formas geométricas

Figuras geométricas para imprimir y pintar

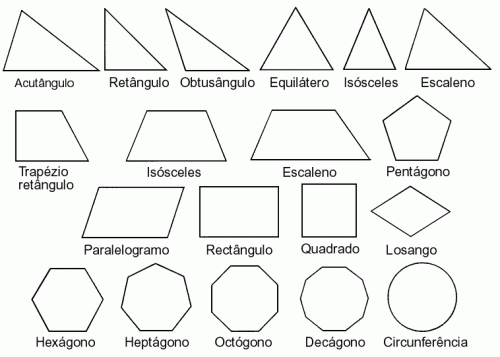
Figuras geométricas para descargar e imprimir

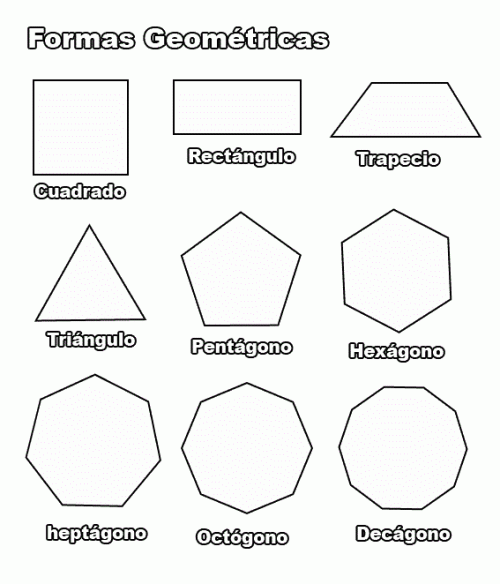
Imagen de figuras geométricas para descargar e imprimir

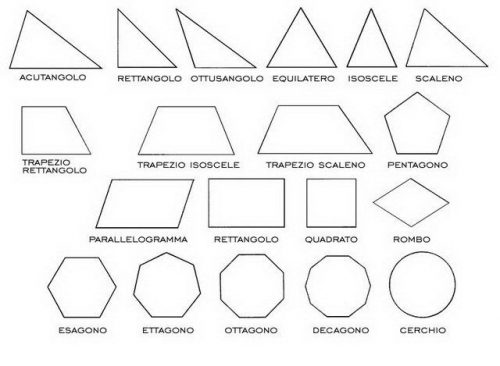
Imagen de formas geométricas para pintar

Formas geométricas planas para descargar y pintas

Tipos de formas geométricas

• Circulo
• Triángulo equilátero
• Triángulo isósceles
• Triángulo escaleno
• Cuadrado
• Rectángulo
• Trapecio
• Pentágono
• Hexágono
• Heptágono
• Octágono
• Nonagon
• Decágono
• Dodecágono
• Polígonos

Formas geométricas para armar

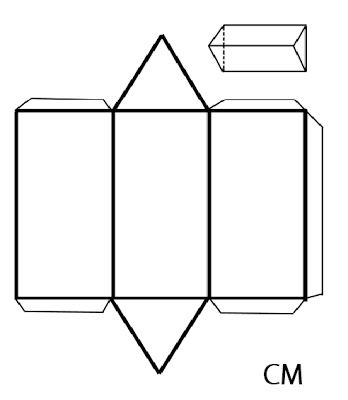
Imagen de figuras geométricas para descargar y armar

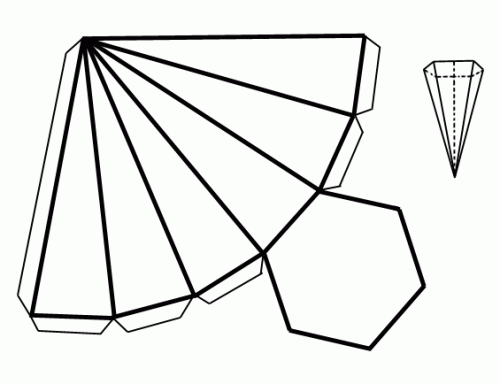
Imagen de formas geométricas para descargar y armar

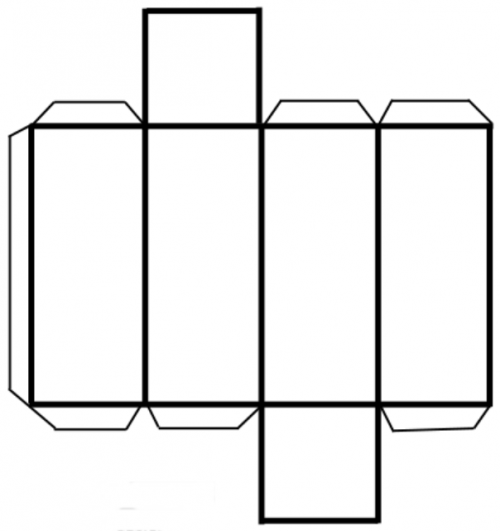
Formas geométricas para descargar y armar

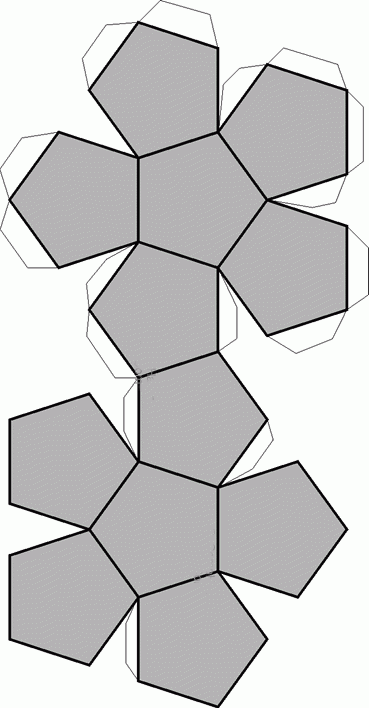
Figuras geométricas para descargar, pintar y armar

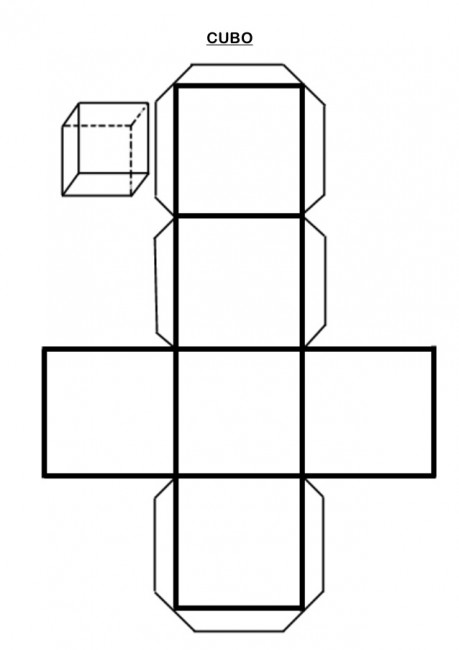
Imagen de cubo para descargar, pintar y armar

Figuras geométricas planas

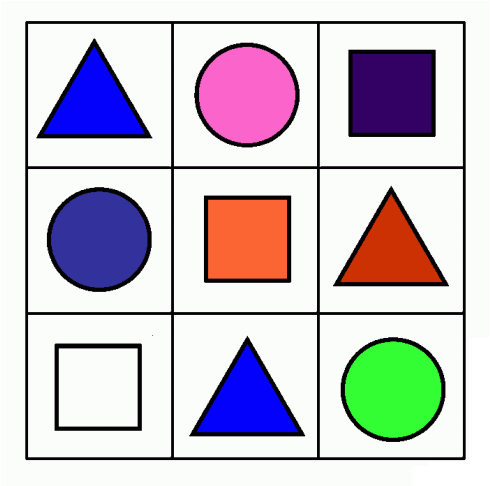
Imágenes de figuras geométricas planas para descargar

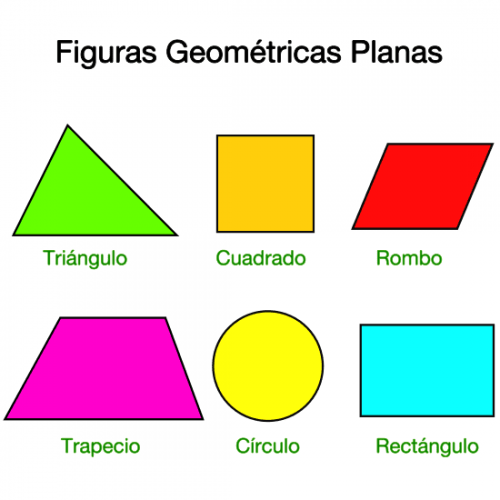
Imágenes de figuras geométricas planas para compartir

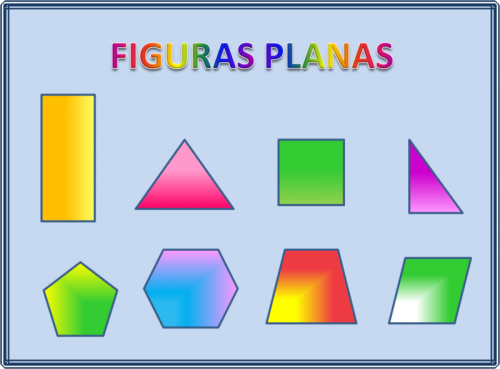
Imágenes de figuras geométricas planas para descargar e imprimir

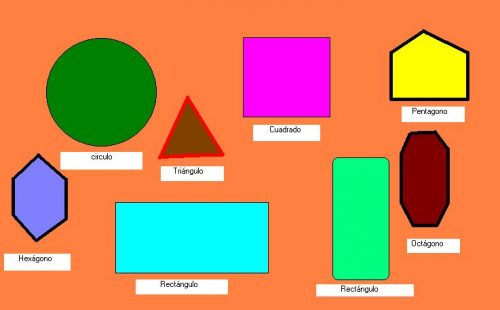
Imágenes de formas geométricas planas para descargar y compartir

Formas geométricas planas para compartir en las redes sociales

Figuras geométricas en 3 dimensiones

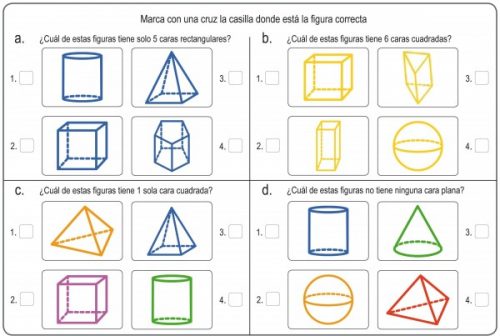
Imágenes de figuras geométricas en 3D para descargar

Imágenes de figuras geométricas en tres dimensiones para imprimir

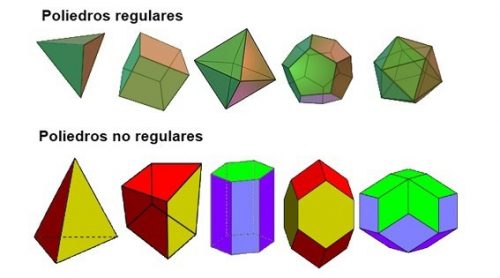
Imágenes de figuras geométricas tridimensionales para descargar

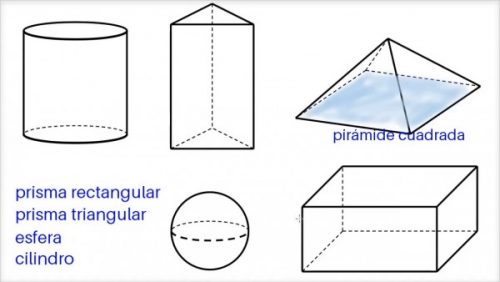
Imágenes de figuras geométricas tridimensionales para colorear

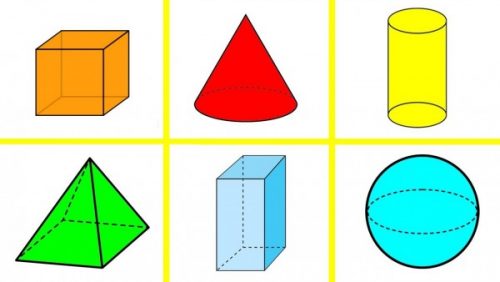
Imágenes de figuras geométricas en tres dimensiones para descargar e imprimir

Figuras geométricas combinadas

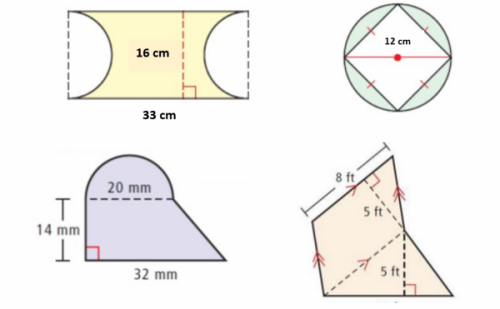
Imágenes de figuras geométricas combinadas para descargar

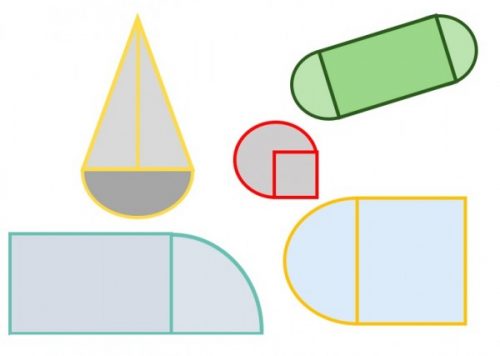
Imágenes de figuras geométricas combinadas para imprimir

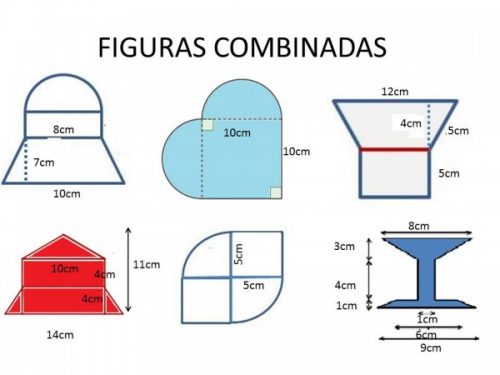
Imágenes de figuras geométricas combinadas para descargar y resolver

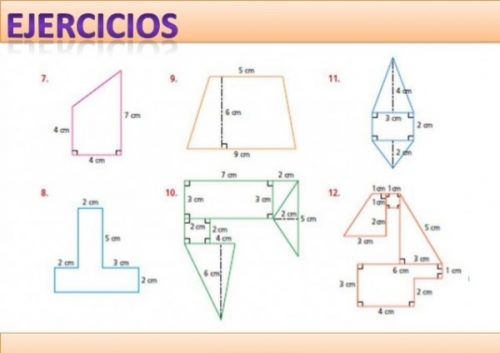
Imágenes de figuras geométricas combinadas para descargar, colorear y resolver

Figuras geométricas para jugar

La geometría es mucho más que líneas, ángulos y formas. Considerado uno de los campos matemáticos más ampliamente aplicados, la geometría es un hilo que une varios conceptos matemáticos. Los divertidos juegos de geometría en línea utilizan objetos cotidianos para enseñar formas, el concepto de 2D y 3D y palabras posicionales. Los niños trabajan sus cerebros, creando patrones geométricos complejos usando formas básicas y practicando divertidos problemas de geometría.

Juego de identificación de formas bidimensionales
Reconocer y nombrar rectángulos, cuadrados, círculos y triángulos presentados en varios tamaños, colores y orientaciones. JUGAR

Lados y esquinas
Desarrolle una comprensión de los atributos con este fabuloso juego. Cuente el número de lados y esquinas en varias formas. JUGAR

Figuras tridimensionales
Reconocer y nombrar cubos, conos, esferas y cilindros presentados en varios tamaños, colores y orientaciones. JUGAR

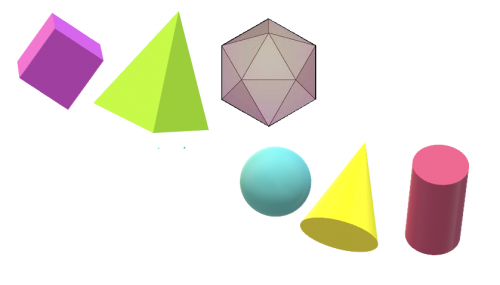
Composición de formas
Juego para colocar varias formas bidimensionales para crear formas más complejas. JUGAR

Formas bidimensionales
Identifique triángulos, rectángulos, cuadrados y trapecios con atributos lados, ángulos, etc. JUGAR

Figuras tridimensionales
Identifique cubos, conos, esferas, cilindros con atributos como superficies curvas y planas, números, caras y esquinas. JUGAR

Aquí hemos llegado al final de nuestro artículo sobre las formas y figuras geométricas. Esperamos que les hayan sido de ayuda y puedan conseguir las imágenes deseadas. Hasta pronto!!!